|
Рассмотрим дифференциальное уравнение
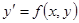 (1) (1)
в предположении, что функция 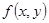 дифференцируема в некоторой окрестности точки дифференцируема в некоторой окрестности точки 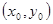 . Задача Коши для дифференциального уравнения (1) формулируется так: найти решение . Задача Коши для дифференциального уравнения (1) формулируется так: найти решение 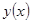 уравнения (1), удовлетворяющее условию уравнения (1), удовлетворяющее условию 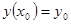 . .
Метод Рунге - Кутта.
Допустим, что функция 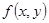 имеет непрерывные частные производные до имеет непрерывные частные производные до 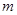 -го порядка включительно, тогда решение -го порядка включительно, тогда решение 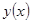 задачи Коши для уравнения (1) будет обладать непрерывными производными до задачи Коши для уравнения (1) будет обладать непрерывными производными до 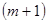 -го порядка включительно и если значение -го порядка включительно и если значение 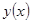 при при 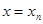 известно, известно, 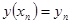 , то справедливо равенство , то справедливо равенство
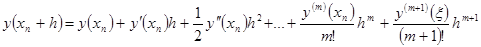 , ,
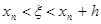 . (5) . (5)
значения входящих сюда производных вычисляются из уравнения (1) последовательным дифференцированием:
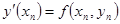 , ,
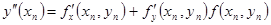 , ,
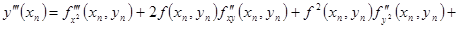
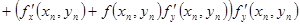 ,… (6) ,… (6)
дифференциальный уравнение mathcad mathconnex
Подставляя значения 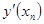 , , 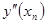 ,…, определенные выражениями (6) в соотношении (5), можно вычислить значение ,…, определенные выражениями (6) в соотношении (5), можно вычислить значение 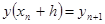 . Однако такой расчет требует вычислений, сложность которых возрастает с увеличением порядка производных. Для сокращения вычислительной работы Рунге предложил значение . Однако такой расчет требует вычислений, сложность которых возрастает с увеличением порядка производных. Для сокращения вычислительной работы Рунге предложил значение 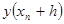 в виде: в виде:
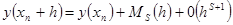 , (7) , (7)
где 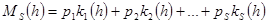 , ,
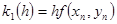 ; ; 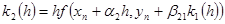 ,…, ,…,
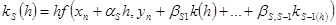 , , 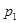 , , 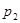 , …, , …, 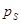 , , 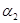 , …, , …, 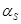 , , 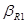 , …, , …, 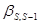 - некоторые параметры. - некоторые параметры.
Формула (3) получается как частный случай формулы (7) при 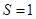 , а формула (4) - при , а формула (4) - при 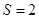 . Рассмотрим вопрос о выборе параметров . Рассмотрим вопрос о выборе параметров 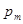 , , 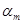 , , 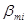 . Для простоты ограничимся случаем . Для простоты ограничимся случаем 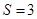 . Введем обозначение: . Введем обозначение:
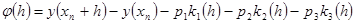 , (8) , (8)
из выражения (7) следует, что
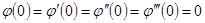 . (9) . (9)
учитывая соотношения (6), из равенства (8) найдем:
Перейти на страницу: 1 2 3
|