|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% | |
Y-пересечение |
0,9103 |
0,0573 |
15,8824 |
0,0000 |
0,7781 |
1,0425 | |
lgX |
0,3938 |
0,0526 |
7,4926 |
0,0001 |
0,2726 |
0,5150 |
|
Наблюдение |
Предсказанное lgY |
Остатки |
Устеп | |
1 |
1,098 |
0,016 |
12,5 | |
2 |
1,243 |
0,036 |
17,5 | |
3 |
1,243 |
-0,067 |
17,5 | |
4 |
1,304 |
0,038 |
20,1 | |
5 |
1,335 |
-0,013 |
21,6 | |
6 |
1,362 |
-0,061 |
23,0 | |
7 |
1,395 |
0,020 |
24,8 | |
8 |
1,423 |
0,054 |
26,5 | |
9 |
1,431 |
-0,016 |
27,0 | |
10 |
1,439 |
-0,008 |
27,5 |
Уравнение линейной модели имеет вид
у = 0,9103 + 0,3938*х
Переходим к исходным переменным х и у, выполнив потенцирование данного уравнения, получим уравнение степенной модели регрессии.
у = 100,9103 *х0,3938= 8,134 *х0,3938
Коэффициент детерминации = 0,862
Коэффициент эластичности Э = b = 0,3938
Средняя относительная ошибка Еотн = 68,45%
График фактических и расчетных данных по степенной модели
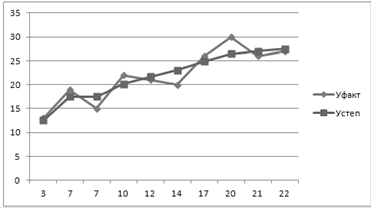
Рис.4
Уравнение показательной модели имеет вид у = abx.
Для построения этой кривой произведем линеаризацию переменных при логарифмировании обеих частей уравнения: lg у = lg а + х*lg b
Обозначим Y= lg у, В= lg b, A=lg a.
Результаты анализа
|
Регрессионная статистика |
| |
Множественный R |
0,9176 | |
R-квадрат |
0,8420 | |
Нормированный R-квадрат |
0,8222 | |
Стандартная ошибка |
0,0488 | |
Наблюдения |
10 |
|
Дисперсионный анализ |
|
|
| |
|
df |
SS |
MS |
F |
Значимость F | |
Регрессия |
1 |
0,101 |
0,101 |
42,626 |
0,000 | |
Остаток |
8 |
0,019 |
0,002 |
|
| |
Итого |
9 |
0,120 |
|
|
|
Перейти на страницу: 1 2 3 4 5 6 7
|
На каком основании людей избирают лидерами, либо позволяют им становиться таковыми? Для объяснения этого явления был разработан ряд теорий, однако последние исследования сосредоточены на так называемых имплицитных теориях лидерства.
Для успешной работы фирмы на рынке необходимо не только определиться с целями, но и понять, как их можно достичь. Для этого надо очень хорошо изучить своего потребителя, а может, даже и создать новый тип потребителя.
Прежде всего менеджеру необходимо определить какой вид карьеры он предпочитает. Это и определит его стратегию. Если он менеджер знает, какое положение хочет занять через пять или даже десять лет, то можно определить направление действий и составить задачи, которых необходимо достичь.