|
ЛАБОРАТОРНАЯ РАБОТА №1
Аналитическое определение экстремума функции одной и нескольких переменных
.1 Функции одной переменной
а) Постановка задачи: исследовать на экстремум функцию вида
y=f(x)=a0+a1*x+a2*x2 (1.1)
б)Необходимое условие экстремума: первая производная функции должна принимать значение, равное нулю.
dQ (x)/ dx=0 (1.2)
Для функции (1.1) получим
d Q (x)/ dx= a1+2a2*x (1.3)*=-a1/2*a2 (1.4)
в)Достаточное условие экстремума : порядок впервые не обращающейся в ноль производной при выполнении условия (1.2) должен быть чётным. Причём, если значение этой производной положительное, то функция Q (x) имеет минимум, а если значение этой производной отрицательное, то функция Q (x) имеет максимум.
Для функции (1.1) имеем:
d Q (x)/ dx =0
d2 Q (x)/ dx2 =2*a2
При выполнении необходимого условия экстремума (1.2) получили порядок впервые не обращающийся в ноль производной четный (он равен 2). Следовательно, функция Q (x) имеет экстремум. Знак второй производной в данном примере определяется знаком коэффициента a2. 
1.2Функция многих переменных
а) Постановка задачи: исследовать на экстремум функцию вида:
Q(x1,x2)=a0+a1*x1 +a2*x12+a3*x2+a4*x22+ a5* x1*x2. (1.5) +a2*x12+a3*x2+a4*x22+ a5* x1*x2. (1.5)
б) Необходимое условие экстремума: частные производные функции должны принимать значения, равные нулю
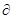 Q (x1, Q (x1, …, xn)/ …, xn)/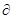 xi=0, i=1,…,n xi=0, i=1,…,n (1.6) (1.6)
Для функции (1.5) получим экстремум функция оптимизация инвестиция
¶ Q (x1, х2)/ ¶x1=0,
2*a2*x1+a5*x2=-a1. (1.7)
¶ Q (x1, х2)/ ¶x2=0,
a5*x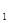 +2a4*x2=-a3 (1.8) +2a4*x2=-a3 (1.8)
По формуле Крамера :
X 1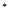 =D1/D, (1.9) =D1/D, (1.9)
X 2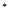 =D2/D (1.10) =D2/D (1.10)
D=4*a2*a4-a52 (1.11)
D1=-2*a1*a4+a3*a5 (1.12)
D2=-2*a2*a3+a1*a5 (1.13)
Систему уравнений (1.7) и (1.8) можно решать методом подстановки.
в)Достаточное условие экстремума.
Разложим функцию Q (x1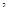 …,xn …,xn ) в ряд Тейлора относительно (x1*,…,xn*) и с учётом (1.6) получим ) в ряд Тейлора относительно (x1*,…,xn*) и с учётом (1.6) получим
DQ(x1*,…,xn*)=0,5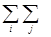 ai,j*zi*zj, (1.14) ai,j*zi*zj, (1.14)
где=Dxi=xi - |xi*|=Dxj=xj-|xj*|
Выражение (1.14 ) называется квадратичной формой.
Составляется матрица из вторых частных производныхj = ¶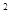 Q(x1,…,xn)/ ¶xi¶xj Q(x1,…,xn)/ ¶xi¶xj
в виде
 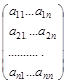 (1.15) (1.15)
Квадратичная форма (1.14) является положительно-определённой, если все диагональные миноры матрицы (1.15) строго положительные. Квадратичная форма (1.14) является отрицательно-определённой, если все нечётные диагональные миноры матрицы (1.15) строго отрицательные, а чётные диагональные миноры матрицы (1.15) строго положительные.
Определение:
Функция Q (x1,…,xn ) имеет минимум, если квадратичная форма (1.14) строго положительная. ) имеет минимум, если квадратичная форма (1.14) строго положительная.
Функция Q (x1,…,xn ) имеет максимум, если квадратичная форма (1.14) строго отрицательная. ) имеет максимум, если квадратичная форма (1.14) строго отрицательная.
Для функции (1.5) имеем:= ¶Q(x1,x2)2/¶x1 2=2*a2
a22= ¶Q(x1,x2)2/¶x2 2=2*a4= ¶Q(x1,x2)2 /¶x1¶x2 = a21= ¶Q(x1,x2)2 /¶x2¶x1 =a5
Ниже приведены значения коэффициентов в уравнениях (1.1)
( таблица 1) и (5) (таблица2)
Таблица 1 |
Значения коэффициентов уравнения 1 | |
№ п/п |
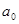 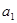 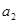 № п/п № п/п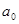 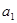 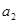
|
|
|
|
|
|
| |
1 |
2 |
-20 |
20 |
29 |
20 |
-38 |
11 | |
2 |
4 |
-22 |
19 |
30 |
18 |
-40 |
12 | |
3 |
6 |
-24 |
18 |
31 |
16 |
-42 |
13 | |
4 |
8 |
-26 |
17 |
32 |
14 |
-44 |
14 | |
5 |
10 |
-28 |
16 |
33 |
12 |
-46 |
15 | |
6 |
12 |
-30 |
15 |
34 |
10 |
-48 |
16 | |
7 |
14 |
-32 |
14 |
35 |
8 |
-50 |
17 | |
8 |
16 |
-34 |
13 |
36 |
6 |
-52 |
18 | |
9 |
18 |
-36 |
12 |
37 |
4 |
-54 |
19 | |
10 |
20 |
-38 |
11 |
38 |
2 |
-56 |
20 | |
11 |
22 |
-40 |
10 |
39 |
20 |
-20 |
20 | |
12 |
24 |
-42 |
9 |
40 |
22 |
-22 |
19 | |
13 |
26 |
-44 |
8 |
41 |
24 |
-24 |
18 | |
14 |
28 |
-46 |
7 |
42 |
26 |
-26 |
17 | |
15 |
30 |
-48 |
6 |
43 |
28 |
-28 |
16 | |
16 |
32 |
-50 |
5 |
44 |
30 |
-30 |
15 | |
17 |
34 |
-52 |
4 |
45 |
32 |
-32 |
14 | |
18 |
36 |
-54 |
3 |
46 |
34 |
-34 |
13 | |
19 |
38 |
-56 |
2 |
47 |
36 |
-36 |
12 | |
20 |
38 |
-20 |
2 |
48 |
38 |
-38 |
11 | |
21 |
36 |
-22 |
3 |
49 |
40 |
-40 |
10 | |
22 |
34 |
-24 |
4 |
50 |
42 |
-42 |
8 | |
23 |
32 |
-26 |
5 |
51 |
44 |
-44 |
6 | |
24 |
30 |
-28 |
6 |
52 |
46 |
-46 |
4 | |
25 |
28 |
-30 |
7 |
53 |
48 |
-48 |
2 | |
26 |
26 |
-32 |
8 |
54 |
50 |
-50 |
2 | |
27 |
24 |
-34 |
91 |
55 |
52 |
-50 |
2 | |
28 |
22 |
-36 |
10 |
56 |
48 |
-50 |
2 |
Перейти на страницу: 1 2 3 4 5 6
|